目录
B+树的局部有序性原理
为什么会出现这种情况呢？这就需要引出 B+ 树的全局有序性和局部有序性这两个关键的概念了。
而想要理解这两个概念，首先我们要从 B+ 树本身的数据结构出发。什么是 B+ 树？
B+ 树的数据结构
既然是 B+树，那么自然是和 B 树摆脱不了关系的，B+树作为 B 树的升级优化版，我们先了解 B 树才能更好深入地理解 B+ 树。
这里我们就简单地介绍一下 B 树和 B+树，更具体的就不在文章中展开来，但是两者的理解还是对理解 MySQL 索引很有帮助的。
什么是 B 树？
在计算机科学中，B 树（B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。
在 B 树中，有两种节点：
- 内部节点（internal node）：存储了数据以及指向其子节点的指针。
- 叶子节点（leaf node）：与内部节点不同的是，叶子节点只存储数据，并没有子节点。
树是一种数据结构。树用多个节点储存元素。某些节点存在一定的关系，用连线表示。二叉树是一种特殊的树，每个节点最多有两个子树。二叉树常用于实现二叉搜索树和二叉堆。 而
AVL 树 是特殊的二叉树，是最早被发明的自平衡二叉查找树。B 树保留了自平衡的特点，但 B 树的每个节点可以拥有两个以上的子节点，因此 B 树是一种多路搜索树。
什么是 B+ 树？
B+ 树是 B 树 的一个升级，它比 B 树更适合实际应用中操作系统的文件索引和数据库索引。目前现代关系型数据库最广泛的支持索引结构就是 B+ 树。
- 有 棵子树的节点中含有 个关键字（即每个关键字对应一棵子树）。
- 所有叶子节点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接。
- 所有的非叶子节点可以看成是索引部分，节点中仅含有其子树（根节点）中的最大（或最小）关键字。
- 除根节点外，其他所有节点中所含关键字的个数最少有 （注意：B 树中除根以外的所有非叶子节点至少有 棵子树）。
总而言之，最主要的关键点就是：
- B+ 树除了叶节点外，是不存储数据的
- B+ 树的叶节点是相互连接的，且所有叶节点处于同一层树
本文就不展开来对这两点做过多详尽的讲解了，但是在后面的是内容是很关键的知识点，牢牢记住！
链表上的树
现在，带着刚才提到的两点，我们来看一张 B+ 树的图
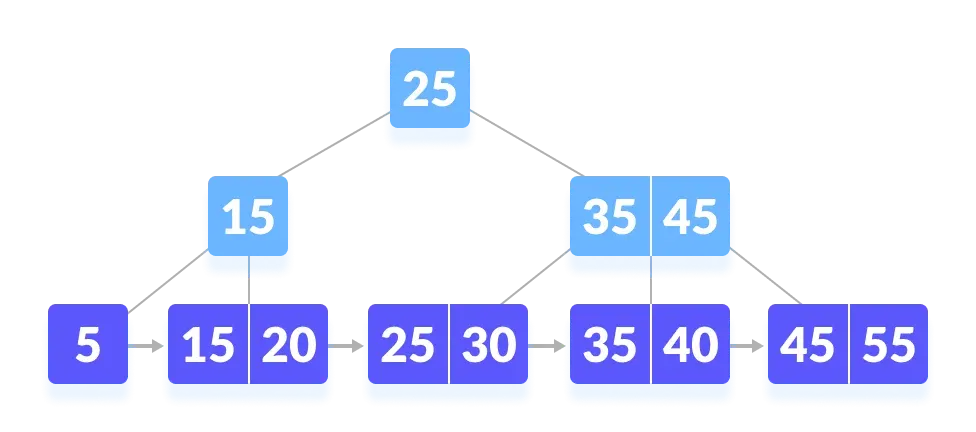首先，我们回顾“B+ 树除了叶节点外，是不存储数据的”这句话。这句话意味着，我们的数据都是存储在最下一层的叶节点，而且在 B+ 树中，叶节点之间都是有指针将各个叶节点连接起来的。
而这，意味着我们可以将 B+ 树最底层的叶节点链表直接抽出来，直接访问这些数据。也就是说，没有上面父节点，这个叶节点链表仍然可以搜索寻找数据。
那么，这些父节点究竟的作用是什么呢？很显然，像是一本厚厚的工具书一样，书本的知识内容都是写在章节中的文段，而不是在首页的目录上。而这些父节点，不存储任何数据，正是 B+ 树中的目录，叶节点链表的目录，帮助我们加速查找。当我们在 B+ 树上搜索数据时，从根节点出发依次进入下一层的父节点，就如同在工具书中，找目录中的一个个章节，然后再去找其中的小结。
局部性有序
现在，我们来说说 B+ 树的有序性。
在刚才的章节中，我们一直在强调 B+ 树的数据存储组织，而没有对其数据有序性进行讨论。前文将 B+ 树分为一个叶节点链表和一个建立于这个链表之上的一个树目录，我们一直在否认这个目录的作用。而在这里，当我们引入 B+ 树中数据的有序性时（毕竟 B+ 树是一个顺序查找树），这个目录的真正意义才会显现。
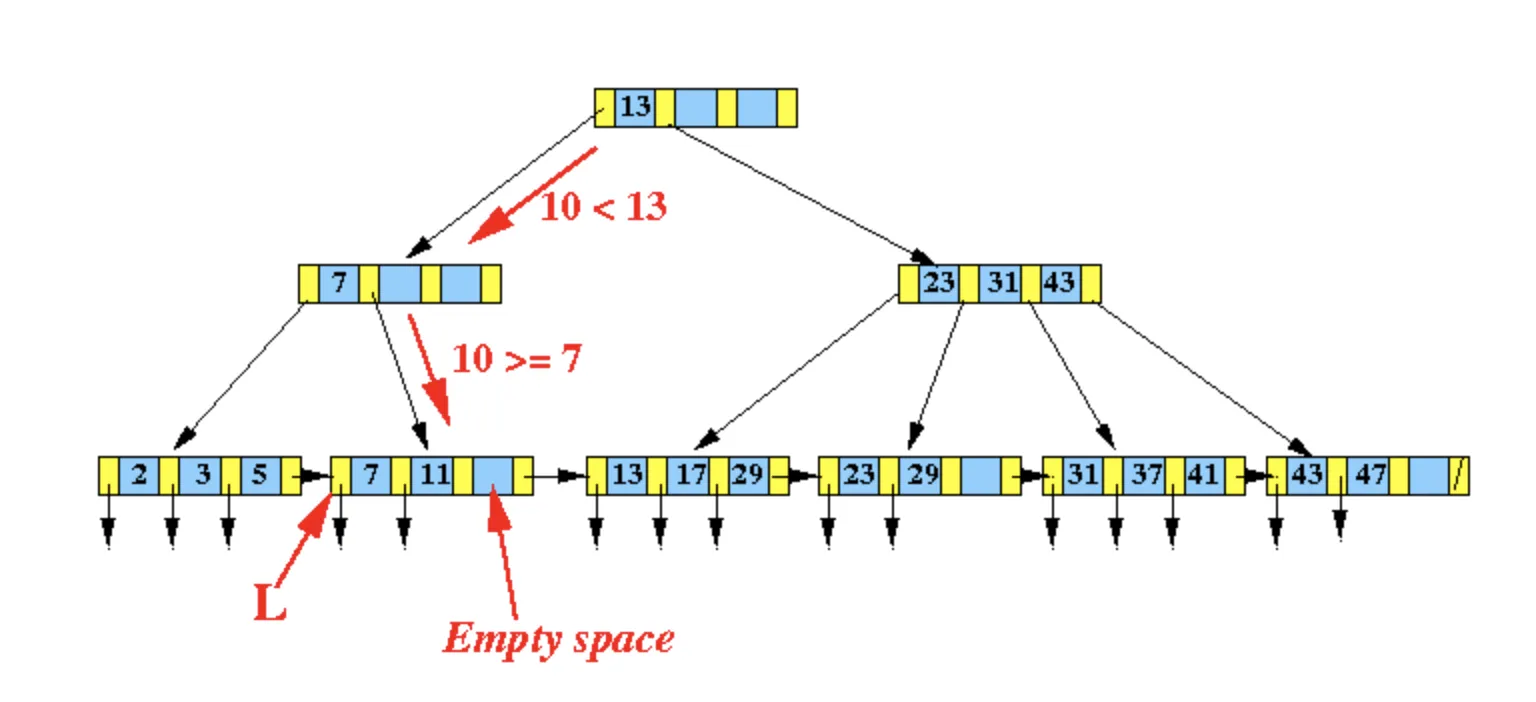回看 B+ 树中的插入过程，我们可以知道数据插入 B+ 树是通过比对树节点的大小来决定插入顺序的。那么这个过程发生多次之后构成的 B+ 树，我们是否可以认为是：在叶节点链表之上的目录树，将链表切割为一个个有序的子链表。而这，也正是 B+ 树的局部性有序的由来。
可能在只有一个索引的时候很难看出来局部性有序的特征，这里我们通过一个联合索引(a, b)来展示。
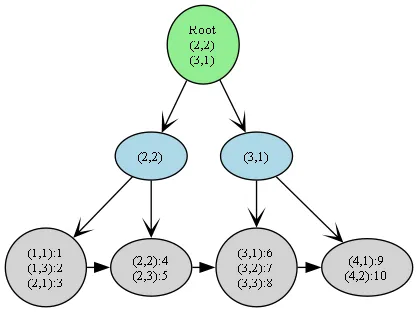
- 在
a相同的情况下，b是有序的 - 但不同
a值之间的b值没有全局顺序
从上面的 B+ 树来看，每一个叶节点中的 b 如果平铺成链表，并不是完全有序的。但是我们如果只局限于单个叶节点中，却又会发现 b 又是有序的。而这，就是 B+ 树的局部性有序性，也是其独特的插入方式和结构特征所导致的数据排序特征。
同时，这也解释了为什么(a, b)索引可以高效处理a = 1 AND b > 2，而(b, a)索引效率低下。
关键理解：B+树的有序性是按索引字段顺序局部有序的，不是全局的。